|
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución.1 Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.
HISTORIA
 La elipse, como curva geométrica, fue estudiada por Menecmo, investigada por Euclides, y su nombre se atribuye a Apolonio de Perge. El foco y la directriz de la sección cónica de una elipse fueron estudiadas por Pappus. En 1602, Kepler creía que la órbita de Marte era ovalada, aunque más tarde descubrió que se trataba de una elipse con el Sol en un foco. De hecho, Kepler introdujo la palabra «focus» y publicó su descubrimiento en 1609. Halley, en 1705, demostró que el cometa que ahora lleva su nombre trazaba una órbita elíptica alrededor del Sol.
La elipse, como curva geométrica, fue estudiada por Menecmo, investigada por Euclides, y su nombre se atribuye a Apolonio de Perge. El foco y la directriz de la sección cónica de una elipse fueron estudiadas por Pappus. En 1602, Kepler creía que la órbita de Marte era ovalada, aunque más tarde descubrió que se trataba de una elipse con el Sol en un foco. De hecho, Kepler introdujo la palabra «focus» y publicó su descubrimiento en 1609. Halley, en 1705, demostró que el cometa que ahora lleva su nombre trazaba una órbita elíptica alrededor del Sol.
ELEMENTOS DE UNA ELIPSE
La elipse es una curva plana y cerrada, simétrica respecto a dos ejes perpendiculares entre sí:
- El semieje mayor (el segmento C-a de la figura), y
- el semieje menor (el segmento C-b de la figura).
Miden la mitad del eje mayor y menor respectivamente.
Puntos de una elipse
Los focos de la elipse son dos puntos equidistantes del centro, F1 y F2 en el eje mayor. La suma de las distancias desde cualquier puntoP de la elipse a los dos focos es constante, e igual a la longitud del diámetro mayor, (PF1 + PF2 = 2a).
Si F1 y F2 son dos puntos de un plano, y 2a es una constante mayor que la distancia F1F2, un punto P pertenecerá a la elipse si se cumple la relación:
donde  es la medida del semieje mayor de la elipse.
es la medida del semieje mayor de la elipse.
 es la medida del semieje mayor de la elipse.
es la medida del semieje mayor de la elipse.Ejes de una elipse
El eje mayor 2a, es la mayor distancia entre dos puntos adversos de la elipse. El resultado constante de la suma de las distancias de cualquier punto a los focos equivale al eje mayor. El eje menor 2b, es la menor distancia entre dos puntos adversos de la elipse. Los ejes de la elipse son perpendiculares entre si.
Excentricidad de una elipse
La excentricidad ε (épsilon) de una elipse es la razón entre su semidistancia focal (segmento que va del centro de la elipse a uno de sus focos), denominada por la letra c, y su semieje mayor. Su valor se encuentra entre cero y uno.
 , con
, con 
Dado que 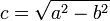 , también vale la relación:
, también vale la relación:
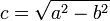 , también vale la relación:
, también vale la relación:
o el sistema:
La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero.3 La designación tradicional de la excentricidad es la letra griega ε llamada épsilon.
(No se debe usar la letra e para designarla, porque se reserva para la base de los logaritmos naturales o neperianos.
Excentricidad angular de una elipse
La excentricidad angular  es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad
es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad  , esto es:
, esto es:
 es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad
es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad  , esto es:
, esto es:
Constante de la elipse
En la figura de la derecha se muestran los dos radio vectores correspondientes a cada punto P de una elipse, los vectores que van de los focos F1 y F2 a P. Las longitudes de los segmentos correspondientes a cada uno son PF1 (color azul) y PF2 (color rojo), y en la animación se ilustra como varían para diversos puntos P de la elipse.
Como establece la definición inicial de la elipse como lugar geométrico, para todos los puntos P de la elipse la suma de las longitudes de sus dos radio vectores es una una cantidad constante igual a la longitud 2a del eje mayor:
- PF1 + PF2 = 2a
En la elipse de la imagen 2a vale 10 y se ilustra, para un conjunto selecto de puntos, cómo se cumple la definición.
Directrices de la elipse
Cada foco F de la elipse está asociado con una recta paralela al semieje menor llamada directriz (ver ilustración de la derecha). La distancia de cualquier punto P de la elipse hasta el foco F es una fracción constante de la distancia perpendicular de ese punto P a la directriz que resulta en la igualdad:
La relación entre estas dos distancias es la excentricidad  de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
 de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
|
Además de la bien conocida relación  , también es cierto que
, también es cierto que  , también es útil la fórmula
, también es útil la fórmula  .
.
 , también es cierto que
, también es cierto que  , también es útil la fórmula
, también es útil la fórmula  .
.
Aunque en la figura solo se dibujó la directriz del foco derecho, existe otra directriz para el foco izquierdo cuya distancia del centro O es -d, la cual además es paralela a la directriz anterior.
Ecuaciones de la elipse
En coordenadas cartesianas
Forma cartesiana centrada en origen
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
donde a > 0 y b > 0 son los semiejes de la elipse, donde si a corresponde al eje de las abscisas y b al eje de las ordenadas la elipse es horizontal, si es al revés, entonces es vertical. El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2ea, siendo e la excentricidad y a el semieje mayor.
Forma cartesiana centrada fuera del origen
En coordenadas polares
Forma polar centrada en origen
En coordenadas polares, con origen en su centro, la ecuación de la elipse es:
Una ecuación más elegante que la anterior (pero que obliga a pre-calcular la excentricidad  ), es:
), es:
 ), es:
), es:(epc 2)
Para ambas ecuaciones a es el semieje mayor, b es el semieje menor de la elipse, θ es el ángulo polar y para la () ε es la excentricidad.
Si no se quiere pre-calcular la excentricidad  convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
 convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
Formas polares centradas en un foco
En coordenadas polares, con el origen en uno de sus focos, la ecuación de la elipse es:
(501)
Para el otro foco:
(502)
En el caso un poco más general de una elipse con un foco en el origen y el otro foco en la coordenada angular 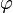 , la forma polar es:
, la forma polar es:
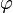 , la forma polar es:
, la forma polar es:(503)}
El ángulo 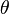 de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas
de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas  es el llamado semi-latus rectum de la elipse, normalmente denotado
es el llamado semi-latus rectum de la elipse, normalmente denotado  . El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.
. El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.
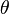 de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas
de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas  es el llamado semi-latus rectum de la elipse, normalmente denotado
es el llamado semi-latus rectum de la elipse, normalmente denotado  . El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.
. El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.
Formas paramétricas
con 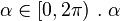 no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre  y θ es
y θ es
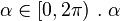 no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre  y θ es
y θ es-
 .
.
La ecuación paramétrica de una elipse con centro en  en la que el parámetro
en la que el parámetro 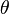 sea concordante con el ángulo polar respecto al centro desplazado
sea concordante con el ángulo polar respecto al centro desplazado  es:
es:
 en la que el parámetro
en la que el parámetro 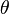 sea concordante con el ángulo polar respecto al centro desplazado
sea concordante con el ángulo polar respecto al centro desplazado  es:
es:
con  . El parámetro
. El parámetro 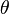 es el ángulo de un sistema polar cuyo origen está centrado en
es el ángulo de un sistema polar cuyo origen está centrado en  .
.
 . El parámetro
. El parámetro 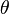 es el ángulo de un sistema polar cuyo origen está centrado en
es el ángulo de un sistema polar cuyo origen está centrado en  .
.
Área interior de una elipse
El área de la superficie interior de una elipse es:
Siendo a y b los semiejes.4
Perímetro de una elipse
El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda especie.
Propiedades notables
La elipse goza de ciertas propiedades asociadas a sus componentes, como se puede ver en Analogía de Michelson y Morley.
La elipse como cónica
 La elipse surge de la intersección de una superficie cónica con un plano, de tal manera que la inclinación del plano no supere la inclinación de la recta generatriz del cono, consiguiendo así que la intersección sea una curva cerrada. En otro caso el corte podría ser una hipérbola o una parábola. Es por ello que a todas estas figuras bidimensionales se las llama secciones cónicas o simplemente cónicas.
La elipse surge de la intersección de una superficie cónica con un plano, de tal manera que la inclinación del plano no supere la inclinación de la recta generatriz del cono, consiguiendo así que la intersección sea una curva cerrada. En otro caso el corte podría ser una hipérbola o una parábola. Es por ello que a todas estas figuras bidimensionales se las llama secciones cónicas o simplemente cónicas.
La elipse como hipotrocoide
 La elipse es un caso particular de hipotrocoide, donde R = 2r, siendo R el radio de la circunferencia directriz, y r el radio de la circunferencia generatriz.
La elipse es un caso particular de hipotrocoide, donde R = 2r, siendo R el radio de la circunferencia directriz, y r el radio de la circunferencia generatriz.
En una curva hipotrocoide, la circunferencia que contiene al punto generatriz, gira tangencialmente por el interior de la circunferencia directriz.
Construcción paramétrica de una elipse
 Se dibujan dos circunferencias concéntricas cuyos diámetros equivalen a la medida de los ejes ortogonales de la futura elipse. Si trazamos segmentos palalelos a los ejes principales X e Y, partiendo del extremo de los radios alineados, la intersección de dichos segmentos son puntos de la elipse.
Se dibujan dos circunferencias concéntricas cuyos diámetros equivalen a la medida de los ejes ortogonales de la futura elipse. Si trazamos segmentos palalelos a los ejes principales X e Y, partiendo del extremo de los radios alineados, la intersección de dichos segmentos son puntos de la elipse.
Anamorfosis de una circunferencia en una elipse
Determinada trasformación de la circunferencia (al deformar ortogonalmente el plano cartesiano asociado a ella), se denomina anamorfosis. Se corresponde con una perspectiva especial. El término anamorfosis proviene del idioma griego y significa trasformar.
En el caso de la circunferencia, si el plano cartesiano se divide en cuadrados, cuando dicho plano se «deforma» en sentido del eje X, el Y, o ambos, la circunferencia se transforma en una elipse y los cuadrados en rectángulos.
Elipses semejantes
Se dice que dos figuras son semejantes cuando se diferencian sólo en el tamaño (pero no en la forma), de tal manera que multiplicando todas las longitudes por un factor dado, se pasa de una figura a la otra. Hay un teorema de utilidad en Física5 acerca de la intersección de una recta con dos elipses semejantes y concéntricas.
|
Explicación: El teorema es cierto, por simetría, en el caso particular en que las elipses dadas sean dos circunferencias concéntricas. Contrayendo o dilatando uniformemente una de las direcciones coordenadas, mediante anamorfosis, podemos transformar cualquier caso en este caso particular, pues todos los segmentos con la misma pendiente cambian su longitud en la misma proporción. Por tanto, puesto que al final del proceso los dos segmentos de la recta tienen la misma longitud, la tenían ya al principio.
No deben confundirse las elipses semejantes con las elipses cofocales.
La elipse en mecánica celeste
En mecánica celeste clásica, dos masas puntuales sometidas exclusivamente a interacción gravitatoria describen una órbita elíptica (o circular 6 ) la una en torno a la otra cuando la órbita es cerrada. Un observador situado en cualquiera de las masas verá que la otra describe una elipse uno de cuyos focos (o centro) está ocupado por el propio observador. La excentricidad y otros parámetros de la trayectoria dependen, para dos masas dadas, de las posiciones y velocidades relativas. Los planetas y el Sol satisfacen la condición de masas puntuales con gran precisión porque sus dimensiones son mucho más pequeñas que las distancias entre ellos. La cinemática de la órbita se rige por las leyes de Kepler.
En la figura pueden verse dos intervalos de tiempo distintos de una órbita elíptica que cumplen la segunda ley de Kepler: "en tiempos iguales una masa en órbita barre con su radio vector áreas iguales". Cuando el "planeta" está más cerca de la "estrella" va más rápido y cuando está lejos va más despacio, pero de tal manera que su velocidad areolar es la misma en ambos casos. Esto significa que las áreas de los sectores elípticos amarillos son iguales y sus arcos t0 t1 se han recorrido en intervalos de tiempo iguales, Δt = t1 - t0. La "estrella" está situada en P, uno de los focos de la elipse.









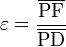

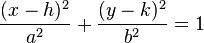

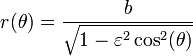

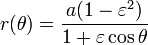


 el semieje mayor y
el semieje mayor y  el menor, es:
el menor, es:





Este comentario ha sido eliminado por el autor.
ResponderEliminar...viaje interestelar aceleración constante (Katherine Coleman Lowe ,,,"Goble" "Johnson", "la chica" matemática genio que traspasó las Puertas de la Historia para entrar en la Leyenda)... sus profesores a los padres cuando aún era una niña prodigio: "en todos mis años de enseñanza nunca he visto una cabeza como la de su hija, tienen que hacerlo, tienen que ver hasta dónde llega...", "decidme donde queréis que caiga en el océano y yo os diré desde donde tenéis que lanzarlo", les decía a los científicos de la NASA cuando los primeros astronautas, a los que le iba la vida en ello, decían "que la chica haga los cálculos"... "El avión pequeño que cayó del cielo", nadie sabía entonces porque, ella descubrió y demostró matemáticamente que habían sido los vórtices de punta de ala de un avión grande que le precedía volando algo más alto, esa turbulencia de otras puntas de ala hizo que aquella avioneta se estellara. Y hasta hoy en que la Aeronáutica sabe lo que Katherine descubrió (en el periódico que dio la noticia no mencionaron su nombre como autora). Pero como era mujer y negra le adjudicaron el mérito a su jefe del departamento y a ella la dejaron como ayudante. Y tantos descubrimientos y cálculos de órbitas que hizo para hacer ir y volver con seguridad a los Apollo de la Luna, a los que llevó literalmente de su mano. A Katherine Johnson le pidieron la Luna y ella no se echó atrás, con poco más que un lápiz, una regla de cálculo y una incipiente informática, que ella tenía que verificar, trazó con precisión las trayectorias que permitirían el aterrizaje... "la NASA nunca olvidará su entusiasmo coraje y liderazgo, y los logros que no podríamos haber alcanzado sin ella"... "triedro de Frenet, el algoritmo de ortogonalización lo prefiero a las coordenadas euclidianas", maravillosa Geometría Analítica, rama de la Geometría que representa las figuras geométricas, planas o tridimensionales, mediante ecuaciones y las sitúa en los ejes de coordenadas x,y,(z)... Katherine y las órbitas elípticas "10,000 cálculos de cosenos...": e, excentricidad >0 y <1, su alargamiento; e=cos B/cos a... elipse, si se define como curva cerrada de la intersección de un plano que corta a un cono sin pasar por su vértice ni su base; a, ángulo del cono entre su eje y generatriz; B, ángulo >a y <90º entre el plano y el eje o altura del cono... El punto pasa/no pasa exacto cuando todavía fórmula no había para saber donde estaba porque iba a ser ella quien la inventara: "...enfocar el problema de forma numérica y no teórica...el método de Euler..." (no era lo mismo caer en cualquier sitio de la estepa cuando Yuri le preguntó a aquella asombrada anciana donde había un telf. para llamar y que vinieran a recogerlo, que tener un barco justo al lado)... "Katherine haz el cálculo"...la respuesta de Katherine: "el punto pasa/no pasa de la re-entrada, es decir pasar de una órbita elíptica a esta trayectoria parabólica exacta, con esta latitud y longitud de caída de la cápsula en el océano margen de error 20 milla², 52 km²"... "Eso me ha gustado", dijo Glenn, "si ella dice que son buenos yo despego"... ((1 milla²=km 1.609344²=2.589988 km² * 20=51.79976 km²))... (Cuando un día un funcionario fue a preguntarle al jefe por esos trabajos, este le dijo "mire hable con Katherine porque ella es en realidad la que lo hace casi todo"). No es de extrañar en un país donde sus religiosos presidentes dicen eso de "que Dios bendiga a los Estados Unidos de América" (y al resto del Mundo que lo parta un rayo)... Aunque tardíos, al fin desde 2015 reconocimientos de la NASA y la nación: Medalla Presidencial Libertad, y en Langley "Centro Katherine G. Johnson", y Medalla de Oro del Congreso. (Sus publicaciones científicas: Wikipedia Katherine Johnson (12)... Legendaria Matemática Katherine Coleman Lowe: Honor y Gloria Eternas... Ya debe haber en el Universo un estrella llamada Katherine.
ResponderEliminarEste comentario ha sido eliminado por el autor.
EliminarEste comentario ha sido eliminado por el autor.
ResponderEliminar...viaje interestelar constante aceleración (la salud por el ajo y el limón)... fina cáscara pelando con guata blanca dejando y Limón a la batidora con 1 Lt de Agua en ayunas <2 horas antes de desayunar, un trago aceite oliva v.e. (en agua para que ácido aceite cuerdas vocales no afecte) DIARIO: jubilación, si gran Aritmética Operación a lápiz y papel hacer puede ser evitar Alzheimer (lo que no se usa se pierde) y si además un Libro de Ciencia y se aprende cada día una línea, o una palabra, y recitar todas las anteriores más la nueva, se aprenderá todo el Libro y después más Libros toda la vida (cerebro genera más neuronas nuevas incluso a 80 años edad)... Zanahoria Sol y 100 grs de uvas-pasas >2 horas hidratadas en 1 Lt de Leche Desnatada (de grasa saturada nada), nueces, y demás alimentos total "100 grs" Proteína (de 1.5 a 2 grs x kilo peso). Antes de levantarse 4x50 Abdominales son fundamentales. Ejercicio Cuerpo y Mente Sana. Naranja Manzana
ResponderEliminarEste comentario ha sido eliminado por el autor.
EliminarEste comentario ha sido eliminado por el autor.
Eliminar...viaje interestelar aceleración constante (do do do)... ¿do nde van los muchos impuestos?: a las Autonosuyas, que no mías, de los políticos rateros que roban la herencia a los herederos, políticos atajo de piojos que comen al Mundo por todas partes. Fuera: consejerías, gobiernos y jerigonzas locales, ayuntamientos y demás político-cuentos. Fuera naciones: 1 Solo Planeta Unido sin naciones, sin guerras y sin fronteras (solo Ciudades con Leyes inflexibles contra delincuentes: los que cometen asesinatos, robos, violaciones, asaltos) de Territorios adheridos a la Unión Universal, UU, con 1 Solo Gobierno Mundial, 1 Solo Idioma, 1 Solo Ejército, 1 Solo Himno y 1 Sola Bandera... ¿do nde van los okupas?: los políticos dicen "a su derecho a la vivienda?, sinvergüenzas. ¿Por qué no okupan el palacio del monarca? Una vivienda no son más que "4 ladrillos" astronómicamente supervalorados para mantener al Pueblo en la inseguridad y sumisión permanente... ¿do nde van los religiosos, monarcas, políticos y patriotas askerrosssos?: a hacer puñetas hay que mandarlos ya de una vez para arreglar el Mundo.
EliminarEste comentario ha sido eliminado por el autor.
ResponderEliminar...viaje interestelar aceleración constante (al planeta azul)... llegan, ven a sus ocupantes y deciden quedarse en la Luna ocultos en la cara oculta. Tendrían que venir por provisiones "al supermercado", tal vez tengan ciudades bajo el suelo oceánico, tal vez se disfrazan de humanos, tal vez controlen la Tierra, o tal vez nada de nada. ¿Dónde están los satélites lunares? No hay ninguno operativo que se sepa, manto de silencio... Han puesto "7000" starlink en órbita Tierra en un momento, han mandado satélites a asteroides... pero a la Luna "noo" que "no interesa todavía" que la gente VEA LA CONTINUA RETRANSMISIÓN EN DIRECTO EN UHD DESDE SATÉLITES EN ÓRBITA BAJA LUNAR (además de instalar farola solar tonyon y cámaras de vigilancia wifi con energía solar por todas partes). Quien manda en la Tierra?: la religión. En cuanto la gente vea que los extra no saben nada de los cuentos miserables religiosos "sin pescado concebida", ya está: adiós a toda religión. 50 años lleva el pontífice tipo "pensándiosselo" a ver como seguir engañando "astroteología" con lo de "es que "los grises" se comen a la gente", religiosos ocultos patrocinadores de todas las películas (financiados por empresas vatic-ano las que tienen el logo con "fondo rojo sangre"). Dejaron en tierra 2 Apollo después de gastarse la millonada que costaron "porque ya no interesaba ir". Radio-secreto Apollo XI: "...te estoy diciendo que aquí afuera hay otra nave espacial. Ellos están al otro lado del cráter ahí debajo acercándose a la Luna junto a nosotros, viéndonos" : "¿Que los están viendo?" : "sí, no estamos solos"...
ResponderEliminarBang Chieng. Tailandia. ("El largo y sinuoso camino de la Química". SciELO Analytics).
Eliminar(La Edad del Bronce comenzó, al menos, en Bang Chieng. Tailandia, hace aprox. "4500 ac" + "2025 dc" = 6525 años (Wikipedia lee SciELO). Todavía hay tribus en la Edad de Piedra. Una Edad comienza en el mismo instante que se descubre algo, no cuando trasciende al resto de la Humanidad).
Eliminar...frenando a un asteroide, el método más expeditivo: colocar "las nucleares" muy cerca de la superficie... "Boom!", en el Espacio, al no haber aire no hay onda expansiva, lo único que le llega es la radiación que volatiliza el material del punto de impacto y produciendo un chorro a reacción que cambia su órbita... (pag. 135-138. Libro "El Asteroide del Fin del Mundo")
ResponderEliminarEste comentario ha sido eliminado por el autor.
EliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarEste comentario ha sido eliminado por el autor.
Eliminar